Answer:
Slope is -200 and y-intercept is at (0, 1200)
The linear equation is:
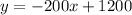
The value of the computer after 4.5 years will be $300.
Explanation:
Value of the new computer is $1200
For tax purposes, the linear depreciation (loss of value) is $200 per year.
So after
 years, total loss of value will be:
years, total loss of value will be:
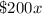
If
 is the declared value of the computer after
is the declared value of the computer after
 years, then the linear equation will be.......
years, then the linear equation will be.......
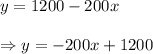
If we compare the above equation with slope-intercept form
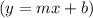 , then we will get:
, then we will get:
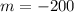 and
and

So, the slope of the line will be -200 and y-intercept will be at (0, 1200)
After 4.5 years means

So when
 ,
,
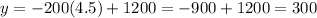
Thus, the value of the computer after 4.5 years will be $300.