Question

What is the slope-intercept form of the equation of the line that contains the points (3, 8) and (6, 5) ?

Answer 1

First for the question you need to find the slope the formula for slope is:

`(y 2 - y1)/(x2 - x1) = \: slope`
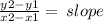
so now you substitute the points you have into this forumla like this:

`(5 - 8)/(6 - 3) = ( - 3)/( - 3) = 1`
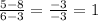
Now we know the slope is 1. We now have to find what b will be in the equation y= mx + b.
To find this out, you must choose one of the points given( you can choose either one you will still get a right answer) For this I will choose point (3,8). In the point 3 is the x value and 8 is the y value. With these numbers and the slope we found we will put them into the equation y = mx + b form it will now look like this:

8 = 1(3) + b now solve

8 = 3 + b
-3 -3

5 = b. Now you have all the numbers to put write the complete equation. The answer is this:

y = x + 5

Answer 2

`\bf (\stackrel{x_1}{3}~,~\stackrel{y_1}{8})\qquad (\stackrel{x_2}{6}~,~\stackrel{y_2}{5}) \\\\\\ slope = m\implies \cfrac{\stackrel{rise}{ y_2- y_1}}{\stackrel{run}{ x_2- x_1}}\implies \cfrac{5-8}{6-3}\implies \cfrac{-3}{3}\implies -1 \\\\\\ \begin{array}c \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-8=-1(x-3) \\\\\\ y-8=-x+3\implies y=-x+11`