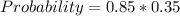Answer:

Explanation:
Giving:
Swimming
![P(Win[Swim])= 65\%](https://img.qammunity.org/2022/formulas/mathematics/high-school/xhysav8cdbzy2i4rtnw3amuauj1hn0nwqd.png)
Running
![P(Win[Run])= 85\%](https://img.qammunity.org/2022/formulas/mathematics/high-school/ud4my0kgbedemxbbii67rzr4wbig1ttbah.png)
Required
Determine the probability of winning at running and losing at swimming
First, we calculate the probability of losing at swimming using
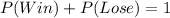
Substitute 65% for P(Win)
![65\% + P(Lose[Swim]) = 1](https://img.qammunity.org/2022/formulas/mathematics/high-school/1m4rkcsj0dno4oium8390fevapuch1s79y.png)
Collect Like Terms
![P(Lose[Swim]) = 1 - 65\%](https://img.qammunity.org/2022/formulas/mathematics/high-school/pdj3k27bhzzp8q2vuc8uu4520n27linj1x.png)
![P(Lose[Swim]) = 35\%](https://img.qammunity.org/2022/formulas/mathematics/high-school/y6n63g40uhmio8g75o394w1erdpd33y4nc.png)
The required probability is then calculated using:
![Probability = P(Win[Run]) * P(Lose[Swim])](https://img.qammunity.org/2022/formulas/mathematics/high-school/ztxp21nju5mgveznynbfbxhtqvey158tya.png)

Convert to decimal