Question

30 points - pls help!

Find the domain and the range of the relation shown on the graph to the right. Use the vertical line test to determine whether the graph is the graph of a function.

Determine the domain of the relation. Select the correct choice below and fill in the answer box to complete your choice.
A.
The domain of the relation is the single value StartSet nothing EndSet
.
​(Type an integer or simplified​ fraction.)
B.
The domain of the relation is the interval
nothing.
​(Type your answer in interval​ notation.)
Determine the range of the relation. Select the correct choice below and fill in the answer box to complete your choice.
A.
The range of the relation is the single value StartSet nothing EndSet
.
​(Type an integer or simplified​ fraction.)
B.
The range of the relation is the interval
nothing.
​(Type your answer in interval​ notation.)
The graph
▼
the graph of a function because a vertical line
▼
can
cannot
be drawn so that it intersects the graph
▼
exactly once.
exactly zero times.
more than once.

Answer 1

1. Find the domain and the range of the relation shown on the graph to the right.

In this exercise, we have the graph of a relation in a Cartesian Coordinate System because it is formed by two perpendicular oriented lines. The horizontal line is called the x-axis while the vertical line is called the y-axis. So the domain of this relation is the set of all x-coordinates while the range is the set of all y-coordinates. Therefore:

• If we walk along the x-axis from left to right we realize that the domain is the set of all real numbers.

• If we walk along the y-axis from down to up we realize that the range is:

`(-\infty,-3) \cup (-1,\infty)`

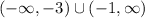
2. Use the vertical line test to determine whether the graph is the graph of a function.

A relation is a function if and only at most one
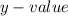`y-value` corresponds to a given
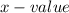`x-value`, meaning that the graph of a function can't match two or more different points with the same x-coordinate, that is, we can't have on the graph of a function two points or more points that are vertically above or below each other. Therefore, a relation is a function if and only if a vertical line intersects the graph of the function at most one point. Following this, we have drawn a vertical line below, so you can see that this line intersects the graph of the function in two points. Therefore, this relation is not a function.