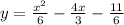Answer:
The correct option is B)
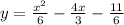
Explanation:
We need to find out the quadratic graph with given focus
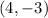 and a directrix
and a directrix
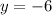
Using the distance formula, we find that the distance between (x,y) and the focus (4,-3) is
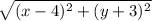 and the distance between (x,y) and the directrix y=-6, is
and the distance between (x,y) and the directrix y=-6, is
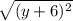
On the parabola, these distances are equal:
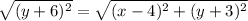

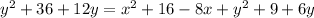
Simplify the above
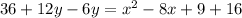
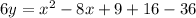

Divide both the sides by 6,
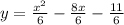
Simplified further,
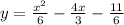
Therefore, the correct option is B)