Question

Alberto is snowboarding down a mountain with a constant slope. the slope he is on has an overall length of 1560 feet. the top of the slope has a height of 4600 feet, and the slope of a vertical drop of 600 feet. It takes him 24 seconds to reach the bottom of the slope.

if we assume that Alberto's speed down the slope is consistent, what is his height above the bottom of the slope at 10 seconds into the Run?

Alberto says that he must have been going 50 miles per hour down the slope. do you agree? why or why not?

Answer 1

For a better understanding of the solution given here please go through the diagram in the file attached.

As we can see from it, BC is the Ski slope whose length is given to be 1560 feet.

AC is the drop of 600 feet.

Since C is the top of the slope, CP will have a total height of 4600 feet.

Now, it has been said that it takes 24 seconds to reach the bottom. In other words it takes 24 seconds to cover the slope which is 1560 feet. Therefore, Alberto's speed will be given as: Speed,
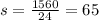`s=(1560)/(24)=65` feet per second.

That means that in 10 seconds Alberto covers 650 feet. Thus, as can be seen from the diagram, RB=
`1560-650=910`.

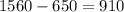Now, if we apply the rules of similar triangles to the triangles ABC and SBR we can see that:

`(RS)/(AC)= (BR)/(BC)`

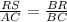
Substituting the values we get:
`(RS)/(600)= (910)/(1560)`

Therefore, we have:
`RS=(910* 600)/(1560)=350` feet.

Thus, Alberto's height above the bottom will be: 4000+350=4350 feet.

Let us measure Alberto's speed in miles/hour.

600 feet=0.113636 miles (approx)

1 hour =3600 seconds

Thus, Alberto's vertical speed will be:
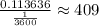`(0.113636)/((1)/(3600))\approx409` miles per hour down the slope which is way above the 50 miles per hour he thinks he has clocked.