Here is my process with mathematical expression interpreter, LaTeX. Full process given below to obtain the values of variable "x" and "y" altogether, solutions to these system of linear equations.
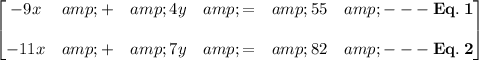
Now here, we should isolate a variable, or take it as a separate form to find the equation, and furthermore substitute the value of variable "y" into the original isolation of "x", to obtain both the solutions for this linear system of equation. Perform this on equation number 1 (Eq. 1).
Subtract the variable attached value by "4y" on both the sides, in current expression.
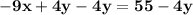
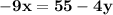
Both the sides, perform a division of value "-9".
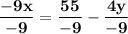
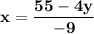
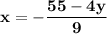
Substitute or just plug the value of newly obtained expression for variable "x" into Equation, numbered as "2" (Eq. 2.) and isolate further for the variable "y", to obtain first solution for this linear equation.
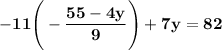
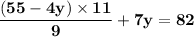
Multiply both the sides by a value of "9".
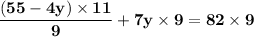
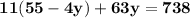


Subtract both the sides by a value of "- 605".
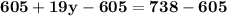
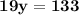
Divide both the sides by "19".
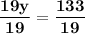

Substitute this variable value of "y = 7" , into our original isolation for variable "x", the expression is to be substituted by that value to complete the solutions for the linear equations. That is:
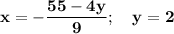
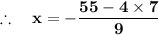
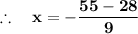
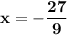

Finalised solutions for these linear system of equations for two components , is:
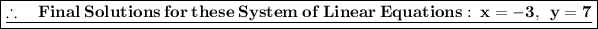
Hope it helps.