Question

33 times a number xxx, subtracted from 181818, is less than -90.?90.Minus, 90, point Write an inequality for the statement above. Find the solution set of the inequality. Write the solution using a fraction or integer.

Answer 1

Let the number be x.

Given: 33 times a number x, subtracted from 18, is less than -90.

we can write this statement in inequality form, i.e,

`18-33x<-90`

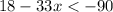
Now, to find the solution set for this inequality:-

`18-33x<-90`

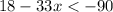
Subtraction poperty of equality states that you subtract the same number from both sides of an equation.

Subtract 18 from both sides,

`18-33x-18<-90-18`

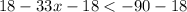
Simplify:

`-33x<-108`

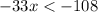
Multiply both sides by -1 (reverse the inequality)

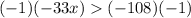`(-1)(-33x)>(-108)(-1)` or

`33x>108`

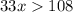
Divide both sides by 33, we get

`(33x)/(33)= (108)/(33)`

Simplify:

`x>(36)/(11)`

Therefore, the solution set for this inequality is,
`((36)/(11) ,\infty )` [

The solution using a fraction or integer is, tex]x>\frac{36}{11}[/tex] 0r
`x>3(3)/(11)`