We are given original equation:
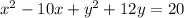
We need to find the enter and radius of a circle using the completing the square method.
The steps are as following :
Step 1 [original equation]: x^2 − 10x + y^2 + 12y = 20 .
Step 2 [group like terms]: (x^2 − 10x) + (y^2 + 12y) = 20
Step 3 [complete the quadratics]: (x^2 − 10x + 25) + (y^2 + 12y + 36) = 20 + (25 + 36).
Step 4 [simplify the equation]: (x^2 − 10x + 25) + (y^2 + 12y + 36) = 64.
Step 5 [factor each quadratic]: (x − 5)^2 + (y + 6)^2 = 8^2
Step 6 [identify the center and radius]: Center = (5, −6) Radius = 8.
Step 6 is incorrect.
The center should be (5,-6).
Replace − 5 with + 5 and replace + 6 with − 6.