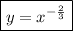Answer:
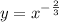
Explanation:
Logarithms
Some properties of logarithms will be useful to solve this problem:
1.
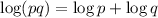
2.
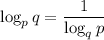
3.
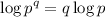
We are given the equation:
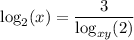
Applying the second property:
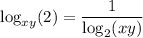
Substituting:
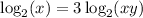
Applying the first property:
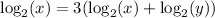
Operating:
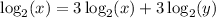
Rearranging:
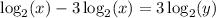
Simplifying:
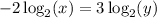
Dividing by 3:
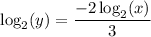
Applying the third property:
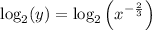
Applying inverse logs: