Answer:
x≈4
Explanation:
We are given that

And we are asked to solve it for x
In order to do that we will use the properties of logarithm
Taking log on both hand sides
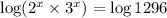 ----------------(A)
----------------(A)
We know that
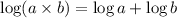
Hence applying this law in (A)
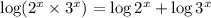
 --------------(B)
--------------(B)
Another property of logarithm says
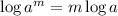
Applying this law in (B)
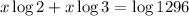
taking x as GCF
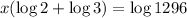
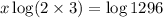
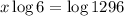
Dividing both sides by \log 6[/tex]
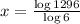
using calculator
log 1296 = 3.1126
log 6 = 0.7781
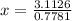
x≈4