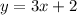1.
The parallel lines have the same a slope.
We have:
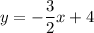
Therefore, the searched line has the equation:
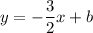
We know, the line passes through point (4,0). Substitute the coordinates of the point to the equation of the line:
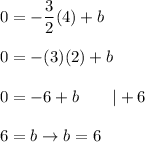
Answer:
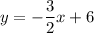
2.
Let
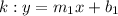 and
and
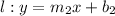
The line l is perpendicular to the line k if and only if
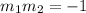
We have
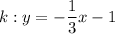
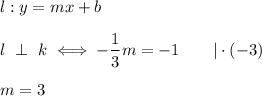
The searched line has the equation:
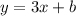
We know, the line passes through point (1,5). Substitute the coordinates of the point to the equation of the line:
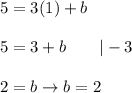
Answer: