Answer:
The answer is the option
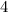
The graph of
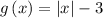 is the graph of
is the graph of
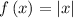 shifted down
shifted down
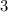 units
units
Explanation:
we have
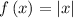
The vertex of the function f(x) is the point
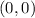
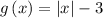
The vertex of the function g(x) is the point
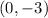
therefore
The rule of the translation of f(x) to g(x) is equal to

That means-------> The translation is
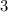 units down
units down