Answer: The correct option is
(A)
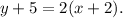
Step-by-step explanation: We are given to use the co-ordinates of the labelled point to find a point-slope equation of the graphed line.
We note from the graph that
the co-ordinates of the labelled point are (-2, -5) and one of the other points that lies on the line is (0, -1).
Since the labelled point also lie on the line, so the slope of the graphed line will be
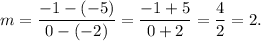
Since the line passes through the point (-2, -5), so the point slope fom of the equation of the line is given by

Thus, the required point-slope form of the equation of the line is
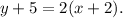
Option (A) is CORRECT.