Question

The H line in Calcium is normally at 396.9nm. however, in a star’s spectrum it is measured at 398,1 nm. How fast is the star moving and is it moving towards the earth

Answer 1

H line of Calcium spectrum is normally given as 396.9 nm

Now from a distant star we measured it as 398.1 nm

So here this change in the wavelength of distant star is due to Doppler's effect of light as per which when source of light moves towards the observer then the frequency of light received will appear different from its actual frequency

So here we can say as per Doppler's effect of light

`(\Delta \\u)/(\\u_0) = (v)/(c)`

`(\\u' - \\u)/(\\u_0) = (v)/(c)`

`((1)/(\lambda) - (1)/(\lambda'))/((1)/(\lambda)) = (v)/(c)`

`(\lambda' - \lambda)/(\lambda') = (v)/(c)`

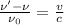
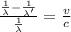
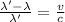
given that

`\lambda' = 398.1 nm`

`\lambda = 396.9 nm`

`c = 3 * 10^8 m/s`

`(398.1 - 396.9)/(398.1) = (v)/(3*10^8)`

`v = 3*10^8 * (1.2)/(398.1)`

`v = 9.04 * 10^5 m/s`

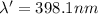
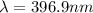
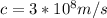
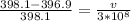
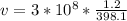
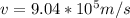
so the start is moving away with speed 9.04 * 10^5 m/s because when wavelength is more than the real wavelength then its frequency is less which mean it is moving away from the Earth