Question

-4/7+(-4/3)
Please help

Answer 1

Hey there!

Answer =
`(-40)/(21)`

Step-by-step explanation:

`-(4)/(7)- (4)/(3)`

So therefore, that is how you found your answer:
`(-40)/(21)`

Answer 2

Here is your equation:

`-(4)/(7) + -(4)/(3)`

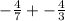
As you can see, the denominators(bottom number) are different. When adding or subtracting fractions, the denominators must be the same.

• To change it, you have to first find the GCM(greatest common multiple), which can be found by listing the multiples of both numbers and finding the common ones.

First list the multiples of both numbers:

`7- 7, 14,21, 28 \\ 3- 3, 6, 9, 12, 15, 18, 21, 24,27`

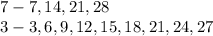
The only common number is 21. That means your new denominator will be 21. Change both fractions so that they have a denominator of 21.

`-(4 * 3)/(7 * 3) = -(12)/(21) \\ \\ -(4 * 7)/(3 * 7) = -(28)/(21)`

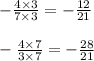
Here is your new equation:

`-(12)/(21) + -(28)/(21)`

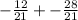
Since both fractions are negative, your answer will be negative. To make things easier, you can just add the two fractions, and add the negative(-) sign.

Add the two fractions:

`(12)/(21) + (28)/(21) = (40)/(21)`

Simplify:

`(40)/(21) \rightarrow 1 (19)/(21)`

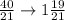
Add the negative(-) sign:

`1 (19)/(21) \rightarrow -1 (19)/(21)`

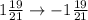
Your answer is
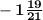`\bf -1 (19)/(21)` or
`\bf -(40)/(21)`

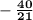
If you have any questions, feel free to ask in the comments! :)