Question

A rectangular prism must have a base with an area of no more than 27 square meters. The width of the base must be 9 meters less than the height of the prism. The length of the base must be 6 meters more than the width of the base. Find the maximum height of the prism.

Let x = the height of the prism
x – 9 = the width of the base
A rectangular prism must have a base with an area of no more than 27 square meters. The width of the base must be 9 meters less than the height of the prism. The length of the base must be 6 meters more than the width of the base. Find the maximum height of the prism.
Let x = the height of the prism
x – 9 = the width of the base
x -3 = the length of the prism

Select the inequality that represents the problem.

x2 – 3 x – 81 ≤ 0

x2 – 3 x – 27 ≤ 0

x2 – 12 x – 27 ≤ 0

x2 – 12 x ≤ 0

Answer 1

D.)

Explanation:

It make the most sense. I also jus got it right on the quiz.

Answer 2

Answer: Choice D)
`x^2 - 12x \le 0`

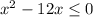
The base has length x-3 and width x-9 which multiplies out to (x-3)(x-9) = x^2-12x+27

This area must be 27 square meters or less, so we set that expression less than or equal to 27

`x^2-12x+27 \le 27`

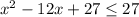
then we subtract 27 from both sides to get the final answer