Question

Find the equation of all tangent lines having slope of -1 that are tangent to the curve y=(9)/(x+1)

Answer 1

`f(x)=\frac9{x+1}\\ f'(x)=-\frac9{(x+1)^2}\\ f'(x)=-1\ \iff\ -\frac9{(x+1)^2}=-1\ \to \ \frac9{(x+1)^2}=1\ \to \ (x+1)^2=9\\ |x+1|=3\ \to \ x+1=3\ \vee\ x+1=-3\\ x_1=2\ \vee\ x_2=-4\\ f(x_1)=f(2)=\frac9{2+1}=3\\ f(x_2)=f(-4)=\frac9{-4+1}=-3`

First tangent line:

`y=f'(x_1)\cdot (x-x_1)+f(x_1)\ \to \ y=-1(x-2)+3\ \to \ y=-x+5`

Second tangent line:

`y=f'(x_2)\cdot (x-x_2)+f(x_2)\ \to \ y=-1(x+4)-3\ \to \ y=-x-7`

Notice: slope of -1 means that both
`f'(x_1), \ f'(x_2)` are equal to -1, so
`f'(x_1)=-1 \ and \ f'(x_2)=-1`

Answer 2

Answer: y = -x + 5 and y = -x - 7 (see attached graph)

Explanation:

y =
`(9)/(x + 1)`

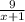
= 9(x + 1)⁻¹

Use the product rule to find the derivative

a = 9 a' = 0

b = (x + 1)⁻¹ b' = -(x + 1)⁻²

ab' + a'b

= 9[-(x + 1)⁻²] + 0[(x + 1)⁻¹ ]

=
`(-9)/((x + 1)^(2))`

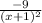
Set the derivative equal to the desired slope of -1 to solve for x

-1 =
`(-9)/((x + 1)^(2))`

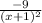
-(x + 1)² = -9

(x + 1)² = 9

√(x + 1)² = √9

x + 1 = +/- 3

x + 1 = 3 x + 1 = -3

x = 2 x = -4

Plug those values into the original equation to solve for y:

y =
`(9)/(x + 1)`

=
`(9)/(2 + 1)`

= 3

(2, 3)

y =
`(9)/(x + 1)`

=
`(9)/(-4 + 1)`

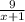
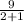
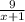
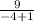
= -3

(-4, -3)

Next, plug in the given slope (-1) and the coordinates above into the Point-Slope formula y - y₁ = m(x - x₁) to find the equations:

m = -1, (x₁ y₁) = (2, 3) m = -1, (x₁ y₁) = (-4, -3)

y - 3 = -1(x - 2) y + 3 = -1(x + 4)

y - 3 = -x + 2 y + 3 = -x - 4

y = -x + 5 y = -x - 7