Question

A diner asks patrons for their preference for waffles or pancakes and syrup or fruit topping.

The table shows the probabilities of results.

Answer 1

`P (Waffles | Syrup)\\eq P(Waffles)`

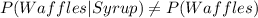
Explanation:

From the table we have to:

Probability of syrup is 0.96

Probability of waffles and syrup is 0.32

P (Waffles | Syrup) = P (Waffles and syrup) / P (syrup)

So:

If this equality is met, the probabilities are dependent, if on the contrary

P (Wafles | Syrup) = P (Wafles) then are independent probabilities.

`P (Wafles | Syrup) = 0.32 / 0.96 = 0.333 \\eq 0.32`

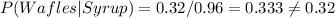
So we have to:

`P (Waffles | Syrup)\\eq P(Waffles)`

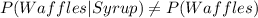
The probabilities are dependent.

Answer 2

Preference for waffies and syrup are dependent events and

`P(waffies\mid syrup)\\eq P(waffies)`

Explanation:

Since we have given that

`P(waffies)=0.34`

`P(syrup\cap waffies)=0.32`

As we know that if A and B are independent it must satisfy ,

`PA\cap B)=P(A).P(B)`

But here,

`P(waffies\cap syrup)\\eq P(waffies).P(syrup)\\0.32\\eq 0.34* 0.96\\0.32\\eq 0.3264`

Hence, they are not independent i.e. they are dependent.

And

`P(waffies\mid syrup)\\eq P(waffies)`

Because,

`P(waffies\mid syrup)\\\\=(P(waffies\cap syrup))/(P(syrup))\\\\=(0.32)/(0.96)\\\\=0.33`

but,

`P(waffies)=0.34`