Answer:
The constant of proportionality between the actual dimensions of the pavers and the model is 9.
The proportionality constant for the area is 81.
Explanation:
To solve this problem, let's transform all quantities to the same units (inches)
The actual dimensions of the pavers are:
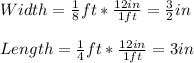
Then we divide the real dimensions between those of the model:
Width:
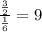
Long =
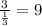
Then, the constant of proportionality between the actual dimensions of the pavers and the model is 9.
Actual length = model length * (9)
The "A" area of a paver is the product of its width multiplied by its length.
So:
(real width) * (real length) = ((9) Model width) * ((9) model length)
(real width) * (real length) =
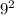 * (Model width) * (model length)
* (Model width) * (model length)
(real area) = 81 * (Model area)
The proportionality constant for the area is 81.