ANSWER
The constant of variation is $
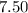
Step-by-step explanation
The constant of variation is the slope of the straight line in the given graph.
The straight line passes through the point
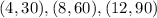
We can use any two of these points to find the slope of this line using the formula,
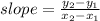
We use
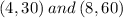

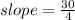
We simplify this to obtain,
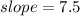
Therefore, the constant of variation is $7.5.
The correct answer is B.