Question

Find the value of y. (7x-7) 63 (3x + 45) (-6)​

Answer 1

b

Explanation:

just did the test like 20 mins ago good look

Answer 2

The value of y is
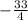`\( -(33)/(4) \)` degrees.

To find the value of y, we can use the properties of the angles in the triangle ACD and the fact that AC = BD.

1. Angle Sum Property of a Triangle:

`\[ \text{Angle CAD} + \text{Angle ACD} + \text{Angle CDA} = 180^\circ \]`

`\[ 63^\circ + (3x + 45^\circ) + (y - 6^\circ) = 180^\circ \]`

2. Simplify and Solve for x:

`\[ 108^\circ + 3x + y - 6^\circ = 180^\circ \]`

`\[ 3x + y = 78^\circ \]`

3. Exterior Angle Property:

`\[ \text{Exterior Angle A} = \text{Angle CAD} + \text{Angle ACD} \]`

`\[ 7x - 7^\circ = 63^\circ + (3x + 45^\circ) \]`

4. Simplify and Solve for x:

`\[ 7x - 7^\circ = 108^\circ + 3x \]`

`\[ 4x = 115^\circ \]`

`\[ x = (115^\circ)/(4) \]`

5. Substitute x back into the Equation from Step 2:

`\[ 3 \left( (115^\circ)/(4) \right) + y = 78^\circ \]`

6. Solve for y:

`\[ (345^\circ)/(4) + y = 78^\circ \]`

`\[ y = 78^\circ - (345^\circ)/(4) \]`

`\[ y = (312^\circ)/(4) - (345^\circ)/(4) \]`

`\[ y = -(33^\circ)/(4) \]`

So, the value of y is
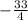`\( -(33)/(4) \)` degrees.