Answer-
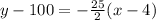
Solution-
We can generate an equation that will represent Eric’s gift card balance, by taking two points from the table and applying two point formula to get the linear relationship between card balance and time.
Taking the time on abscissa and card balance on ordinate, the two points would be (2, 125), (4, 100)
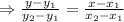
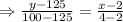
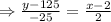
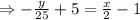
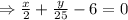
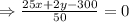
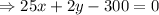
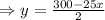
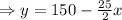
This is the equation for the Eric’s gift card balance.
Comparing this equation with general slope-intercept equation of the line, we get
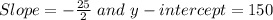
Applying point-slope formula taking point as (4, 100), we get
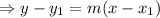
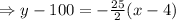
This is the desired equation.