Question

PLEASE HELP ASSIGNMENT DUE TODAY NEED TO PASS

1)
You have 2 lines. The first goes through points (6, 2) and (4, 6). The second goes through points (5,-1) and (1, 1). These lines are:

A) perpendicular

B) parallel

C) horizontal and vertical

D) none of the above

2) You have 2 lines. The first goes through points (7, 0) and (4, 6). The second goes through points (1, 1) and (5,3). These lines are:

A) perpendicular

B) parallel

C) horizontal and vertical

D) none of the above

Answer 1

1. D

2. A

Explanation:

To determine the type of line, find the slope.

• Slopes which are the same are parallel
• Slopes which are negative reciprocals are perpendicular
• Slopes which are undefined (0 in the denominator) are horizontal.
• Slopes which are 0 are vertical.

1. Find the difference in y values over the difference in x values. Calculate the slope using the formula:

`(y_2-y_1)/(x_2-x_1) = (6-2)/(4-6)=(4)/(-2)=-2`

`(y_2-y_1)/(x_2-x_1) = (1--1)/(1-5)=(2)/(-4)=(-1)/(2)`

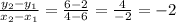
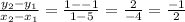
These are reciprocals of each but not the negative or opposite signs of each other. This is none.

2. Find the difference in y values over the difference in x values. Calculate the slope using the formula:

`(y_2-y_1)/(x_2-x_1) = (6-0)/(4-7)=(6)/(-3)=-2`

`(y_2-y_1)/(x_2-x_1) = (3-1)/(5-1)=(2)/(4)=(1)/(2)`

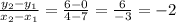
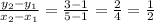
These are reciprocals of each and the negative or opposite signs of each other. These are perpendicular.