Question

1. Find the length of a rectangular lot with a perimeter of 124 feet if the length is two more than twice the width.

2. Find the length of a rectangular lot with a perimeter of 50 feet if the length is five more than the width.

Answer 1

ANSWER TO QUESTION 1


Let the width be

`w`
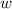
units.



Twice the width will be


`2w`

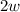
Two more than twice the width will be


`2w + 2`



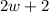
We were told that the length is 2 more than twice the width. This means that,


`l = 2w + 2`


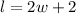
This implies that,


`w = (l - 2)/(2) - - eqn(1)`


The formula for finding the perimeter of a rectangle is given by:



`perimeter = 2w + 2l - - eqn(2)`




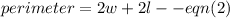
We substitute 124 for the perimeter and equation (1) into equation (2)




`124 = 2( (l - 2)/(2) ) + 2l`


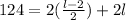
This implies that,


`124 = l - 2 + 2l`


`\Rightarrow 124 + 2 = l + 2l`




`\Rightarrow 126 = 3l`




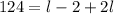
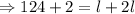
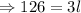
We divide both sides by 3 to obtain,



`l = 42`

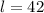
Therefore the length is 42 feet.





ANSWER TO QUESTION 2


Let the width be

`w`


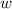
units.


Five more than the width will be



`w + 5`


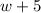
We were told that the length is 5 more than the width. This means that,



`l = w + 5`


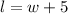
We make w the subject to obtain,



`w = l - 5 - - eqn(1)`



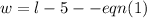
The perimeter is given by,


`perimeter = 2w + 2l - - eqn(2)`

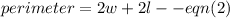
We substitute 50 for the perimeter and equation (1) into equation (2)



`50 = 2(l - 5) + 2l`

Dividing through by 2 gives,



`25 = l - 5 + l`




`\Rightarrow 25 + 5 = l + l`




`\Rightarrow 30 = 2l`


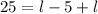
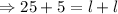
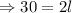
We divide both sides by 2 to get,


`l = 15`


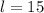
Therefore the length is 15 feet.