Question

Which reason completes the proof below?

Given: ABCD is a parallelogram. ModifyingAbove upper A upper C with bar bisects Angle B C D and Angle B C D.

Prove: ABCD is a rhombus.
A. Opposite sides of a parallelogram are congruent.
B. Sides of a rhombus are congruent.
C. Diagonals of a parallelogram bisect each other.
D. Diagonals of a rectangle are congruent.

Answer 1

Answer: opposite sides of a parallelogram are congruent

Explanation:

Answer 2

Observe the figure given.

Given: ABCD is a parallelogram.

To prove: ABCD is a rhombus

Statement

1. ABCD is a parallelogram. AC bisects
`\angle BCD, \angle BAD`.

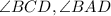Reason: Given

2.
`\angle 1 \cong \angle 2, \angle 3 \cong \angle 4`

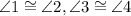
Reason: Definition of an angle bisector

3.
`AC \cong AC`

Reason: Reflexive property of congruence

4.
`\Delta ABC \cong \Delta ADC`

Reason: ASA Postulate

5.
`AB \cong AD, BC \cong DC`

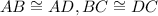
Reason: corresponding parts of congruent triangles are equal.

6.
`AB \cong CD, BC \cong AD`

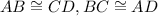
Reason: Opposite sides of the parallelogram are congruent.

7.
`AB \cong AD \cong BC \cong CD`

Reason: Transitive property of congruence

8. ABCD is a rhombus

Reason: Definition of rhombus