Question

Find the coordinates of the other endpoint of the? segment, given its midpoint and one endpoint.? (Hint: Let? (x,y) be the unknown endpoint. Apply the midpoint? formula, and solve the two equations for x and? y.) midpoint ?( negative 11 ?11?, 18 18?), endpoint ?( negative 5 ?5?, 10 10?)

Answer 1

We are given mid-point (-11, 18).

One end point (-5, 10).

`\mathrm{Midpoint\:of\:}\left(x_1,\:y_1\right),\:\left(x_2,\:y_2\right):\quad \left((x_2+x_1)/(2),\:\:(y_2+y_1)/(2)\right)`

Let us take coordinate of other end points is (x,y).

Therefore,

`\left(x_1,\:y_1\right)=\left(-5,\:10\right),\:\left(x_2,\:y_2\right)=\left(x,\:y\right)`

`\left((x_2+x_1)/(2),\:\:(y_2+y_1)/(2)\right) =\left((x-5)/(2),\:(y+10)/(2)\right)`

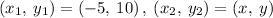
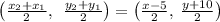
Given mid point (-11, 18).

Therefore,

`\left((x-5)/(2),\:(y+10)/(2)\right) = (-11, 18)`

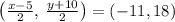
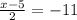`(x-5)/(2)=-11` and
`(y+10)/(2) = 18`

Multiplying both sides by 2 in both equations, we get

x-5 = -22 and y+10 =36.

x = -22+5 and y = 36-10

x = -17 and y = 26.

Therefore, corrdinates of other end point is (-17, 26).