Answer:
The radius of the gear is, 0.286624204 m
Explanation:
A gear is driven by a chain that travels 90 m/min. If it makes 50 revolutions per minute. then find the radius of the gear
let angular velocity be
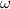 , velocity be v and radius be r.
, velocity be v and radius be r.
Given:
Angular velocity
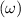 =50 revolutions per minute
=50 revolutions per minute
1 revolution =
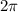 radian
radian
50 revolution=
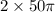
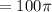 radian
radian
therefore,
 radian per minute
radian per minute
and velocity(v) = 90 meter per minute
Use formula: Velocity(v)= radius(r)
 angular velocity
angular velocity
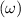
then, we write above formula as :
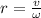
Substitute the value of v and
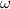 to solve for r: the constant value of pi i.e,
to solve for r: the constant value of pi i.e,
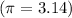
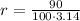
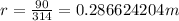 [as radian is unit less]
[as radian is unit less]