Question

Tom has just received a new job offer he is told that his salary will be 75,000.00 per year he is also told that his salary will probably be 83,000.00 in four years assume that y= toms salary amount in dollars and x= the number of years worked

1. use data given to find rate of change, or the salary increase per year (hint: commute the slope.)
2. use data given and the slope vale from step 1 to write the slope- intercept form of the line.
3. based on your equation from step 2 what will toms salary be in ten years?

Answer 1

`y_(0)=75,000` when x=0.

`y_(4)=83,000` when x=4.

1.Rate of change=
`Slope=(y_(4)- y_(0))/(4-0)\\\\= (83,000-75,000)/(4-0)\\\\=(8,000)/(4)\\\\=2000`

2. Slope intercept form of salary and number of years

`(y-75,000)/(x-0)=2000` →[as slope =2,000]

→y-75,000=2,000 x

→y= 2000 x+ 75,000

3.Tom salary after 10 years ,

put x=10

y=2000×10+75,000

y=20,000+75,000

y=$95,000

Salary after 10 years=$95,000

Answer 2

Here,

x = number of years worked,

y = salary in dollars.

Tom is getting $75,000 of salary right now, so for this case,

x₁ = 0,

y₁ = 75000

Tom will be getting a salary of $83,000 after 4 years from now, so for this case,

x₂ = 4,

y₂ = 83000

1.

Rate of change of salary = slope of the line joining (x₁, y₁), ( x₂, y₂)

`Slope= (y_2-y_1)/(x_2-x_1)`

`\Rightarrow Slope= (83000-75000)/(4-0)`

`\Rightarrow Slope=2000`

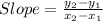
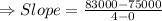
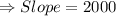
∴ The salary increase per year is $2000.

2.

Equation of the line in slope-intercept formula,

`y-y_1=m(x-x_1)`

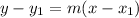
Putting x₁ = 0, y₁ = 75000, we get

`y-75000=2000(x-0)`

`y-75000=2000x`

`y=75000+2000x`

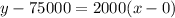
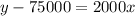
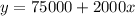
3.

Putting x = 10, we can compute the value of y to get the salary after 10 years.

`y=75000+2000(10)`

`y=75000+20000`

`y=95000`

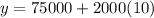
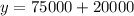
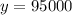
∴ Tom's salary in ten years will be $95,000