Question

What is the solution of the equation over the complex numbers

Answer 1

`2i√(3)`

`-2i√(3)`

Explanation:

`x^2 + 12`

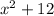
First set the equation to 0

`x^2 + 12`

`x^2 + 12 = 0`

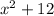
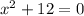
Second, get the 12 on the right side of the equal sign by adding a -12 to each side

`x^2 + 12 = 0`

`x^2 + 12 + (-12) = 0 -12`

`x^2 = -12`

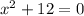
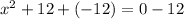
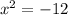
Square root both sides of the equal sign.

`x^2 = -12`

`√(x^2) = √(-12)`

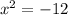
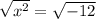
Take the square root on left sides of the equal sign.

`√(x^2) = √(-12)`

`x = √(-12)`

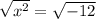
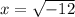
Take the square root on the right side of the equal sign. Remember
`√(-1) = i`

`x = √(-12)`

`x = √(4)*√(-1)√(3)}`

`x = 2i√(3)`

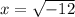
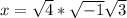
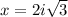
AND

`x = -2i√(3)`