Answer:
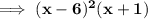
Explanation:
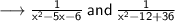
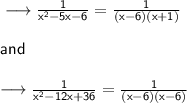

Therefore, the least common denominator is (x - 6)²(x+1).
Additional information:
# How to solve middle splitting term ?
Step 1) : First of all notice that term is in standard form.
For eg :- 6x + 2x² + 5 = 2x² + 7x + 5
Step 2) : Multiply with first and last term.
2 × 5 = 10
Step 3) : Next we have multiply got the answer 10 and subtract or add we have got the answer 7.
- 1 × 10 = 10 and 10 - 1 = 9 or 10 + 1 = 11
- 2 × 5 = 10 and 5 - 2 = 3 or 5 + 2 = 7
Now, we have got the term. We have multiply 2 and 5 got the answer 10 and we have add got the answer 7.
Step 4) : Attach the factor into the removal of 7x
2x² + 5x + 2x + 5
Step 5) : Simplify it
- 2x² + 5x + 2x + 5
- x(2x + 5) + 1(2x + 5)
- (2x + 5)( x + 1)
Step 6) : We have got the answer
