Question

a particle moves along the x axis with an acceleration of a=18t, where a has units if m/s2. if the particle at time t=0 is at the origin with a velocity of -12 m/s, what js its position at t=4.0s?

Answer 1

Position at t= 4 seconds is 144 m

Step-by-step explanation:

It is given that acceleration, a = 18 t, where t is the time.

We know that Velocity,
`v = \int { a} \, dt`

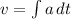
Substituting value of a,

Velocity,
`v = \int {18t} \, dt=(18t^2)/(2) +c=9t^2+c`

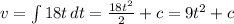
We know that at t = 0, v = -12 m/s

So,
`9*0^2+c=-12\\ \\ c=-12m/s`

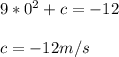
So velocity,
`v = (9t^2-12)m/s`

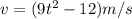
We also know that displacement,
`x = \int { v} \, dt`

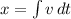
Substituting value of v,

Displacement,
`x=\int {(9t^2-12)} \, dt=(9t^3)/(3) -12t+c=3t^3-12t+c`

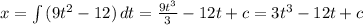
We know that at t = 0, particle is at origin, x =0.

So,
`0=3*0^3-12*0+c\\ \\ c=0`

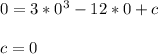
Displacement,
`x = 3t^3-12t`

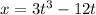
At t = 4 seconds

`x = 3*4^3-12*4=192--48=144m`

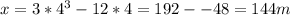
Position at t= 4 seconds is 144 m