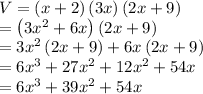Answer:
Volume =
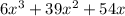
Explanation:
Prism is an object which has two bases which are parallel to each other and other faces are parallelograms .
Rectangular prism is a three dimensional figure which has 6 faces which are all rectangles .
Let l be the length of rectangular prism , w be the width of prism and h be the height of prism .
Then volume of rectangular prism is equal to
 .
.
We will also use formula:
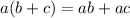
Here,
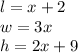
Therefore,
volume of rectangular prism is calculated as follows: