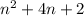Answer:
The n-th term for the sequence will be:
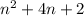
Explanation:
Given sequence is: 7, 14, 23, 34, 47. 62, 79, ........
The n-th term of a quadratic sequence is:
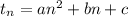
For
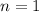 ....
....

For
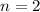 ....
....

For
 ....
....
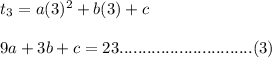
Subtracting equation (1) from equation (2), we will get......

Subtracting equation (2) from equation (3), we will get.......

Now, subtracting equation (4) from equation (5)...........

Plugging this
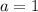 into equation (4), we will get....
into equation (4), we will get....
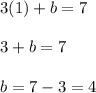
Now, plugging
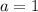 and
and
 into equation (1) .........
into equation (1) .........

Thus, the n-th term for the sequence will be: