Answer:
WZ = √26 and WXYZ = 8+2√26
Explanation:
We can see from the diagram that WZ goes from (-2, 4) to (-3, -1). Using the distance formula, we have
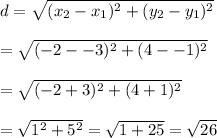
Since WZ and XY are the same length, then these two sides together give us a length of
√26+√26 = 2√26.
Since WX is a horizontal segment, we find the distance of the segment by finding the distance between the x-coordinates:
2--2 = 4
WX and ZY are the same length, so this gives us
4+4 = 8
This makes the total perimeter 8 + 2√26 units.