Question

Simplify the fraction and state the excluded value(s).


`(7x^2+4x-20)/(5x+10)`

Answer 1

`\color{skyblue}{\boxed{\tt{ANSWER:}}}`

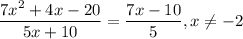
General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction
8. Left to Right
9. Algebra I

Terms/Coefficients

Factoring

Calculus

Discontinuities

• Removable (Holes)
• Jump (Piece-wise functions)
• Infinite (Asymptotes)

^_^ ❤

Answer 2

`\displaystyle (7x^2 + 4x - 20)/(5x + 10) = (7x - 10)/(5), x \\eq -2`

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Algebra I

• Terms/Coefficients

• Factoring

Calculus

Discontinuities

• Removable (Holes)
• Jump (Piece-wise functions)
• Infinite (Asymptotes)

Explanation:

Step 1: Define

`\displaystyle (7x^2 + 4x - 20)/(5x + 10)`

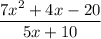
Step 2: Simplify

1. [Frac - Numerator] Factor quadratic:
   `\displaystyle ((7x - 10)(x + 2))/(5x + 10)`
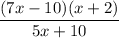
2. [Frac - Denominator] Factor GCF:
   `\displaystyle ((7x - 10)(x + 2))/(5(x + 2))`
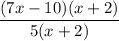
3. [Frac] Divide/Simplify:
   `\displaystyle ((7x - 10))/(5), x \\eq -2`

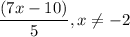
When we divide (x + 2), we would have a removable discontinuity. If we were to graph the original function, we would see at x = -2 there would be a hole in the graph.