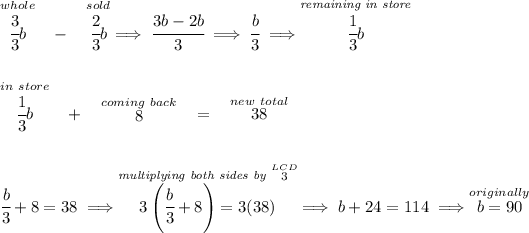Question

Please explain how you got it also ​

Answer 1

a WHOLE is always simplified to "1", and we can use any denominator for that, so 5/5 is 1, and 7/7 = 1, and
`\cfrac{4}{4}\implies \cfrac{113}{113}\implies \cfrac{1000000}{1000000}\implies \text{\LARGE 1}whole`

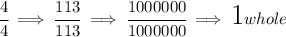
so hmmm for this case we'll be use thirds or namely the denominator of 3, so a whole bunch of basketballs was originally 3/3 of "b", "b" was the whole amount, so originally we had 3/3, but then during the day we sold 2/3 of them, so we were left with 3/3 - 2/3 = 1/3, and then 8 came back, because they were deflated or something, now the store has a total of 38 basketballs.

`\stackrel{whole}{\cfrac{3}{3}b}~~ - ~~\stackrel{sold}{\cfrac{2}{3}b}\implies \cfrac{3b-2b}{3}\implies \cfrac{b}{3}\implies \stackrel{\textit{remaining in store}}{\cfrac{1}{3}b} \\\\\\ \stackrel{in~store}{\cfrac{1}{3}b}~~ + ~~\stackrel{coming~back}{8}~~ = ~~\stackrel{new~total}{38} \\\\\\ \cfrac{b}{3}+8=38\implies \stackrel{\textit{multiplying both sides by }\stackrel{LCD}{3}}{3\left( \cfrac{b}{3}+8 \right)=3(38)}\implies b+24=114\implies \stackrel{originally}{b=90}`