Can I get some help on these please

Question

asked Feb 21, 2019 232k views

1 Answer

ThreeFatCat · Answer 1 · 2019-02-27T03:03:35+0000

Simply multiply the equation by 6, in order to get rid of the denominators:

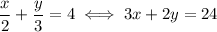
$(x)/(2)+(y)/(3) = 4 \iff 3x+2y=24$

We have to rearrange the equation in the form

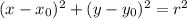
(x-x_0)^2+(y-y_0)^2=r^2

So that
is the radius, and
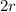will be the diamater. We have to complete the squares: rewrite the equation as

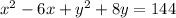
x^2-6x+y^2+8y=144

You can see that
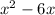x^2-6x is the beginning of
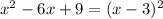
x^2-6x+9 = (x-3)^2

Similarly,
y^2+8y is the beginning of
y^2+8y+16 = (y+4)^2

So, if we add 16 and 9 to both sides, the equation becomes

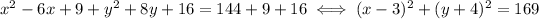
$x^2-6x+9+y^2+8y+16=144+9+16 \iff (x-3)^2+(y+4)^2=169$

So, now we know that
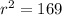r^2=169 , and thus the radius is 13, so the diameter is 26.