Question

Naomi starts the engine on her small private airplane. The engine drives a propeller with a radius of 8 feet and its centerline 13 feet above the ground. At idle, the propeller rotates at a constant speed of approximately 700 revolutions per minute. The height of one propeller tip as a function of time is given by h = 13 + 8 sin(700t), where h is the height in feet and t is the time in minutes. Use degrees to find h when t = 4 minutes.

Answer 1

5.13 feet

Explanation:

Engine is driving the propeller with a radius of 8 feet and its centerline 13 feet above the ground.

And the speed is 700 revolutions per minute, the height of one propeller tip as a function of time is given by:

`h=13+8 \sin(700t)`

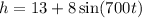
We have been asked to find the value of height, 'h', when t=4 minutes.

Plugging the value of time, 't', in the equation, we already know that we need to use degrees (not radians) we get:

`h=13+8 \sin (700 * 4)`

`h=13+8 \sin (2800)`

`h=13+8 * (-0.984)`

`h=13+(-7.872)`

`h=13-7.872`

`h=5.128\approx 5.13`

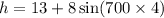
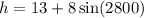
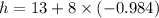
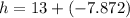
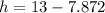
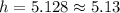
So the height of one propeller tip at t=4 minutes is 5.13 feet.