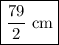Question

The perimeter of a rectangle is 150 cm. the length is 4 cm greater than the width find the width and length

(please explain how you did this or show) (thank you)

Answer 1

Let's call the width of our rectangle
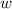`w` and the length
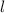`l`. We can say
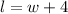`l = w + 4`, since the length is equal to 4 cm greater than the width.

Also remember that the perimeter of a rectangle is the sum of two times the width and two times the length, or
`P = 2l + 2w`. To solve this problem, we can substitute in the information we know, as shown below:

`150 = 2(w + 4) + 2w`

`150 = 4w + 8`

`142 = 4w`

`w = (71)/(2)`

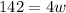
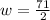
Now, we can substitute in the width we found into the formula for length, which is
`l = w + 4`:

`l = (71)/(2) + 4`

`l = (79)/(2)`

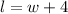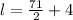
The width of our rectangle is
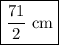`\boxed{(71)/(2) \,\, \textrm{cm}}` cm and the length of our rectangle is
`\boxed{(79)/(2) \,\, \textrm{cm}}`