Question

Bob is driving along a straight and level road toward a mountain. At some point on his trip, he measures the angle of elevation to the top of the mountain and finds it to be 23°29'. Find the height of the mountain to the nearest foot if Bob is 16,194.6 feet from the center of the mountain at the base.

Answer 1

The line from Bob to the Peak of the mountain is the hypotenuse, and Bob's distance from the center base of the mountain is one leg, and the height of the mountain is the other leg. The 23o29' angle is between the hypotenuse and the leg from Bob to the Base (16194.6 ft). The side opposite to the angle is the height of the mountain.

The relevant trig function, then, is the tangent:

Tangent x = opposite side/adjacent side

Here the adjacent side is 16,194.6 feet and the opposite side is the height of the mountain. So

Tan(23.483o) = height/(16,194.6)

Solve for the height.

Answer 2

The height of mountain= 197,185 foot.

Explanation:

We are given that Bob is driving along a straight and level towards a mountain.

The measure of angle of elevation to the top pf the mountain =
`23^(\circ)29'`

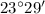
The distance of Bob from the centre of the mountain base =16,194.6 feet.

We have to find the height of mountain.

Let height of the mountain=h feet

In a triangle ABC

AB=h feet

BC=16,194.6 feet

`\angle C= 23^(\circ)29'`

`29'=(29)/(60)=0.48`

`\angle C=23+0.48=23.48^(\circ)`

`1^(\circ)=60'`

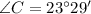
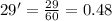
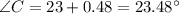
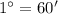
We know that
`tan\theta=(perpendicular )/(base)`

Substitute the values then we get

`tan23.48^(\circ)=(h)/(16194.6)`

`12.176* 16194.6=h`

`h=197,185.4 foot`

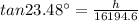
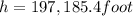
h=197,185 foot

Hence, the height of mountain= 197,185 foot.