Question

Factor the following expression.

10x^5 + 5x^3 - 14x^2 - 7

A. (5x^3 + 7) (2x^2 -1)
B. (5x^4 + 7) (2x -1)
C. (5x^4 - 7) (2x + 1)
D. (5x^3 - 7) (2x^2 + 1)

So, I took the test already a million times already and I keep failing because of questions similar to this. I'd appreciate if you also explained the process instead of just giving an answer. Thank you!

PS: (5x^4 - 7) (2x + 1) is not the answer.

Answer 1

10x^5 + 5x^3 - 14x^2 - 7

= 5x^3(2x^2 + 1) - 7(2x^2 + 1)

= (5x^3 - 7)(2x^2 + 1)

Answer is D

(5x^3 - 7)(2x^2 + 1)

Answer 2

D.

Explanation:

Let's use common factor gruping terms. We have that we have a common factor between the two left terms and another common factor between the two right terms. Then,

for the two left terms we take the common divisor, in this case 5 and the x with the minimun exponent, that is 5x^3.

for the two right terms we take the common divisor, in this case -7 and the x with the minimun exponent, in this case the -7 has no x so we don't include it in the common factor.

`10x^5 + 5x^3 - 14x^2 - 7 = 5x^3(2x^2+1)-7(2x^2+1)`

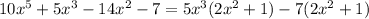
Now, we use common factor again, this time the common factor will be
`2x^2+1`:

`10x^5 + 5x^3 - 14x^2 - 7 = 5x^3(2x^2+1)-7(2x^2+1)= (2x^2+1)(5x^3-7)`.

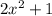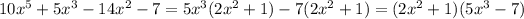Then, the answer is D.