Question

020 (part 1 of 3) 10.0 points

A tennis ball is dropped from 1.39 m above the
ground. It rebounds to a height of 0.968 m.
With what velocity does it hit the ground?
The acceleration of gravity is 9.8 m/s². (Let
down be negative.)
Answer in units of m/s.
021 (part 2 of 3) 10.0 points
With what velocity does it leave the ground?
Answer in units of m/s.
022 (part 3 of 3) 10.0 points
If the tennis ball were in contact with the
ground for 0.0125 s, find the acceleration
given to the tennis ball by the ground.
Answer in units of m/s².

Answer 1

The tennis ball hit the ground at a speed of approximately
`5.22\; {\rm m\cdot s^(-1)}`.

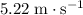The tennis ball bounced away from the ground at a speed of approximately
`4.36\; {\rm m\cdot s^(-1)}`.

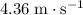The average acceleration of the tennis ball during the contact was approximately
`766\; {\rm m\cdot s^(-2)}`.

Step-by-step explanation:

If an object of mass
`m` is travelling at a speed of
`v`, the kinetic energy
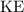`\text{KE}` of that object will be
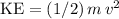`\text{KE} = (1/2)\, m\, v^(2)`. At a height of
`h` above the ground, the gravitational potential energy
`\text{GPE}` of that object will be
`\text{GPE} = m\, g\, h`.

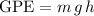If the drag on the tennis ball is negligible, energy will be conserved:

`\begin{aligned}& \text{GPE at initial height} \\ &= \text{KE right before hitting the ground}\end{aligned}`.

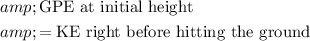In particular, if the tennis ball was released from a height of
`h`, its speed
`v` right before landing will ensure that
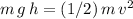`m\, g\, h = (1/2)\, m\, v^(2)`. Rearrange to obtain
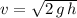`v = √(2\, g\, h)`. Since the tennis ball was released from a height of
`h = 1.39\; {\rm m}`, the speed of the ball right before landing will be:

`\begin{aligned}v &= √(2\, g\, h) \\ &= \sqrt{2\, (9.8\; {\rm m\cdot s^(-2)}) \, (1.39\; {\rm m})} \\ &\approx 5.22\; {\rm m\cdot s^(-1)}\end{aligned}`.

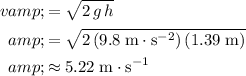The same reasoning applies when the tennis ball bounces off the ground:

`\begin{aligned}& \text{KE right after leaving the ground} \\ &= \text{GPE at max height after bouncing upward}\end{aligned}`.

If the tennis ball bounced off the ground at a speed of
`v`, the height
`h` that this tennis ball will reach should also satisfy
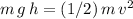`m\, g\, h = (1/2)\, m\, v^(2)`. Rearrange to obtain
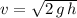`v = √(2\, g\, h)`. Since the tennis ball reached a height of
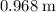`0.968\; {\rm m}`, it would have bounced off the ground at a speed of:

`\begin{aligned}v &= √(2\, g\, h) \\ &= \sqrt{2\, (9.8\; {\rm m\cdot s^(-2)}) \, (0.968\; {\rm m})} \\ &\approx 4.36\; {\rm m\cdot s^(-1)}\end{aligned}`.

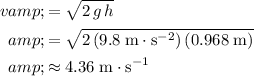Acceleration measures the rate of change in velocity. The velocity of this tennis ball was downward right before landing, at approximately
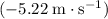`(-5.22\; {\rm m\cdot s^(-1)})` (the negative sign indicates the direction of velocity.) The velocity of this ball points upward after bouncing back, at approximately
`4.36\; {\rm m\cdot s^(-1)}`.

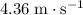Hence, the change in the velocity of this tennis ball will be:

`\begin{aligned} \Delta v &= v_(1) - v_(0) \\ &\approx4.356\; {\rm m\cdot s^(-1)} - (-5.220\; {\rm m \cdot s^(-1)}) \\ &\approx 9.576\; {\rm m\cdot s^(-2)}\end{aligned}`.

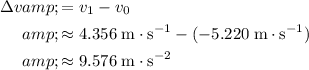Since this change in velocity required a duration of
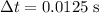`\Delta t = 0.0125\; {\rm s}`, the average acceleration of this tennis ball would have been:

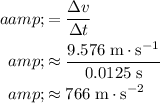`\begin{aligned} a &= (\Delta v)/(\Delta t) \\ &\approx \frac{9.576\; {\rm m\cdot s^(-1)}}{0.0125\; {\rm s}} \\ &\approx 766\; {\rm m\cdot s^(-2)} \end{aligned}`.