Answer:
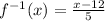
Explanation:
Given:
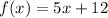
Replace f(x) with y:
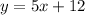
Switch variables and solve for y:
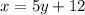
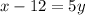
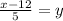
Simplify:
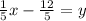
Replace y with f^-1(x):
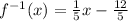
Therefore, the inverse function for
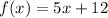 is
is
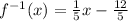 .
.
Notice how in the graph attached of the inverse functions that they are symmetric about the line y=x. This is a crucial characteristic of inverse functions.