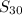 = 1455
= 1455
generate a few terms of the sequence using
 = 3n + 2
= 3n + 2
 = ( 3 × 1) + 2 = 5
= ( 3 × 1) + 2 = 5
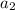 = (3 × 2) + 2 = 8
= (3 × 2) + 2 = 8
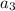 = (3 × 3 ) + 2 = 11
= (3 × 3 ) + 2 = 11
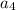 = (3 × 4 ) + 2 = 14
= (3 × 4 ) + 2 = 14
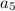 = ( 3 × 5 ) + 2 = 17
= ( 3 × 5 ) + 2 = 17
the terms are 5, 8, 11, 14, 17
these are the terms of an arithmetic sequence
sum to n terms is calculated using
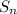 =
=
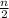 [ 2a + (n-1)d]
[ 2a + (n-1)d]
where a is the first term and d the common difference
d = 8 - 5 = 11 - 8 = 14 - 11 = 3 and
 = 5
= 5
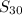 =
=
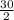 [( 2 × 5) + (29 × 3) ]
[( 2 × 5) + (29 × 3) ]
= 15( 10 + 87) = 15 × 97 = 1455