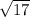Answer:
The answer is 2
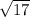 , we need to use the distance between point formula; I recommend you search in the internet another examples.
, we need to use the distance between point formula; I recommend you search in the internet another examples.
Explanation:
We need to calculate the distance between points, so we need to use the formula d=
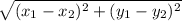
You can use Janes house (-5,-2) or friends house like (3,-4) point 1 or 2, it is the same way.
when we substitute in the formula
:
d =
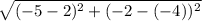
d=
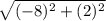
d=
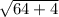 =
=
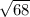
We need to reduce this result, so we need to find two number wich on of those can we solve the square root, if we divide 68/4 we find:
d=

And 4 has exact square root result, so the result in:
2