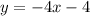Question

What is the equation of a line perpendicular to

y =

`(1)/(4) x \: - 3`
that passes through point (-2, 4)?

Answer 1

Since the given line


`y = ( 1)/(4) x - 3`

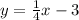
has slope

`= (1)/(4)`


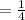
The equation of the line perpendicular to it must have a slope which is the negative reciprocal of ,

`(1)/(4)`
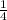
The slope of the perpendicular line

`= ( - 1)/( (1)/(4) ) = - 4`
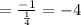
Using the slope intercept form,


`y = mx + c`
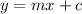
We substitute

`- 4`
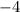
This implies that,

`y = - 4x + c`
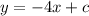
Since


`(-2,4)`
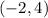
lies on this line , it must satisfy its equation.

That is


`4 = - 4( - 2) + c`


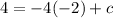
This implies that


`4 = 8 + c`

`4 - 8 = c`

`c = - 4`

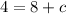
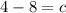
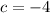
The line therefore has equation,


`y = - 4x - 4`