Answers:
- Domain:

- Range:
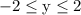
- The relation is not a function
========================================================
Step-by-step explanation:
The domain is the set of possible x values. The left-most point occurs when x = -2, while the right-most point is when x = 2. Therefore, x is between -2 and 2 in which we write
 . Both endpoints are included.
. Both endpoints are included.
-----------
The range is the set of possible y values. The possible y values are in the interval
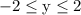 since y = -2 is the smallest y can get, and y = 2 is the largest it can get. Visually we look at the lowest and highest points respectively to find the span of y values.
since y = -2 is the smallest y can get, and y = 2 is the largest it can get. Visually we look at the lowest and highest points respectively to find the span of y values.
-----------
This relation is not a function because it fails the vertical line test.
It is possible to pass a single vertical line through more than one point on the curve. For example, the vertical line through x = -1 goes through the points (-1,1) and (-1,-1)
Phrased another way: The input x = -1 leads to more than one output.
A function is only possible if each input in the domain leads to exactly one output.