Question

Halley's comet ranges from 0.59 to 35.3 astronomical units from the sun, which is at one focus of the comet's elliptical orbit (an astronomical unit is Earth's mean distance from the sun). Explain by sketching an ellipse. Then write an equation for the orbit.

Answer 1

We have the comet's range from 0.59 to 35.3 astronomical units.

Now the question says that Halley's comet is orbiting in an elliptical orbit.

Here we will not convert AU (astronomical unit) into miles or kilometers.

Let the perhelion (the point in the orbit of a planet, asteroid, or comet at which it is closest to the sun) = 0.59 AU

Let the aphelion (the point in the orbit of a planet, asteroid, or comet at which it is farthest from the sun) = 35.09 AU

1. Now, the length of the major axis is given by:

`= 0.59 + 35.30= 35.89`

so, length of the semimajor axis
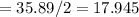`= 35.89 / 2 = 17.945` AU= 'c'

And the distance from the center of the ellipse to the Sun

`= a= 17.945-0.59 = 17.355` AU

2. [ The co-ordinates of the Sun = (17.355 , 0 )

We need to find the length of the semi-minor axis i.e 'b'.

`b= √(c^2-a^2)`

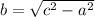
Putting the values of 'c' and 'a' in the equation we get:

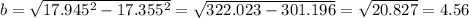`b= √(17.945^2-17.355^2)=√(322.023-301.196)=√(20.827)=4.56` AU

Therefore, our equation for the orbit of the comet Halley is given by:

(We will use the general equation of the ellipse and plug in the values of 'a' and 'b'. )

`(x^2)/(17.355^2) +(y^2)/(4.56^2) =1`

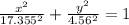
NOTE: For the convince we have not converted AU into miles or kilometers.