Question

Jose is adding mulch to an existing round flower bed. The length of the rubber edging around the flower bed is 25.12 feet. What is the area that jose needs to cover with mulch?

Answer 1

The perimeter of the square rubber edging is 25.12 feet.

Get the length of each side.

Since the formula for getting a square's perimeter is 4s, divide the perimeter by 4.

25.12 ÷ 4 = 6.28

Each side is 6.28 feet long.

The diameter of the circular flower bed inside the rubber edging is equal to the length of one side of the rubber edging.
(Diameter: 6.28 ft.)

Radius is half of the diameter.
(Radius: 3.14 ft)

Use the formula below to get the area of the circular flower bed.


`a = \pi \: r ^(2)`
a = (3.14) (3.14 ft) (3.14 ft)
= (3.14) (9.8596 ft^2)

The answer would be:

`30.959144 \: ft ^(2)`

♧

Answer 2

The area of Jose needs to cover with mulch is 50.24 feet.

Explanation:

Consider the provided information.

Jose is adding mulch to an existing round flower bed.

The length of the rubber edging around the flower bed is 25.12 feet.

That means the circumference of the bed is 25.12 feet.

Now to find the area first calculate the radius.

The circumference of a circle is:
`C=2\pi r`

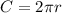
Substitute the respective values in the above formula.

`25.12=2\pi r` Use π=3.14

`25.12=2* 3.14 r`

`25.12=6.28 r`

`4=r`

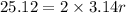
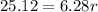
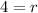
Hence, the value of r is 4 feet.

Now find the area by using the formula:

The area of a circle is:
`A=\pi r^2`

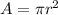
Substitute the respective values in the above formula.

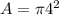`A=\pi 4^2` Use π=3.14

`A=3.14 * 16`

`A=50.24`

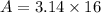
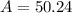
Hence, the area of Jose needs to cover with mulch is 50.24 feet.